How to Calculate the Cost of Universal Basic Income (Hint: It's Not As Easy As You Might Think)

I've written about this before, about how the cost of universal basic income is its net cost, not its gross cost, but because this question of the cost of UBI is so frequently raised, and so frequently misunderstood, I'm going to attempt to explain this in an alternative way in the hopes people might come to understand it at a deeper level, and therefore be less likely to fall for misinformation.

Claim

The cost of universal basic income (C) is the dollar amount of the UBI (D) multiplied by the number of people receiving it (N).

Equation

C = D x N

Rating: FALSE

Explanation

First of all, it's important to understand that simple multiplication doesn't calculate the cost of UBI. The reason is because UBI is not the usual kind of program where some people receive a cash benefit while higher taxes are imposed on a different group of people, or where people receive a non-cash benefit in exchange for higher taxes. With UBI, everyone receives cash, and everyone (or at least most everyone) pays some amount of cash too. It's possible to implement UBI completely disconnected from taxes or any kind of tax reform, but it's also highly unrealistic to consider that special case, and only that special case, when costing a UBI plan. Any UBI plan is most likely to include new taxes and not just cash, unless increased inflationary pressure is the goal of a nation adopting it.

Consider the example of a tax credit paired with a tax increase. If the government were to create a new $1,000 tax credit, that would increase someone's disposable income after taxes by $1,000. That is unless it also increased their income tax rate a few percentage points such that they owed $1,000 more in taxes. In that case, they wouldn't gain or lose anything. The net result would be $0 more in disposable income and $0 more in taxes, despite the new tax credit and new tax increase.

Would it make any sense to say the cost of that new $1,000 tax credit for that one person was $1,000? From the perspective of that person, and the perspective of their government, there was no change in disposable income and no change in government tax revenue. It was just a (+1000) and (-1000) added to a ledger, which of course is equivalent to just adding a zero.

It would be like if I gave you $10, then asked for it back, got it back, and then said the amount of my money had been reduced by $10 because I gave you $10. Obviously, that would be incorrect. You might even think I had memory problems.

When someone claims that the cost of UBI is simply the amount of UBI times the number of people, the mistake they're making is to ignore the existence of any accompanying tax reform, which must be taken into account in order to figure out what people are actually getting, and the amount the government is newly taxing.

So in order to calculate the total cost of UBI (C), one must first start with the cost of UBI for one person. That cost can be expressed by the amount of UBI (D) minus the amount of new taxes imposed (T).

C = D - T

To visualize this, again imagine I handed you $10, but then asked for $5 back instead of $10. In this case, my income would decrease by $5 and yours would increase by $5, which is equivalent of course to my just handing you $5 and asking for nothing back. In either case, the cost is $5, not $10.

Note: to denote this is one person we are talking about, it helps to add a subscript to the variables in the equation before we continue.

C₁ = D₁ - T₁

Now let's calculate the cost of UBI for two people. To do that, we'll need to figure out the cost for each person, and then add those two differences together.

C₁ = D₁ - T₁
C₂ = D₂ - T₂

C = C₁ + C₂

At this point, I hope it's now apparent that the cost of UBI is a summation of the individual differences between the amount of UBI received and the amount of new taxes paid across all recipients of UBI.

C = C₁ + C₂ + C₃ + C₄ + C₅ ... + C_n

This equation can now be simplified via sigma notation.

_i=1Σⁿ = D_n - T_n

Thus in math speak, UBI's cost is really the summation of a finite arithmetic series.

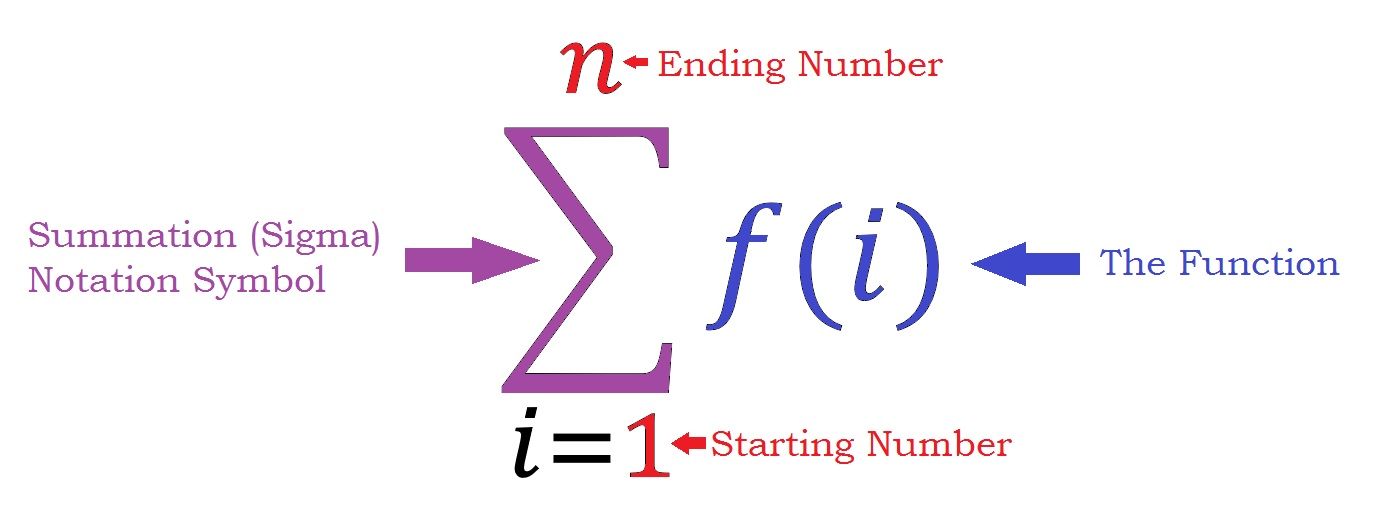
However, there's still one more important detail to consider, which is the difference between the positive and negative results. The summation of all net recipients where D > T will be a positive number, and the summation of all net tax payers where D < T will be a negative number. It is these two separate sums that together convey the most useful information about the cost of UBI.

The summation of all positive values of C is the net total amount of UBI distributed across all net recipients. That number can be understood as the cost of UBI to the government.

The summation of all negative values of C is the total amount of new taxes paid by net payers. That number can be understood as the cost of UBI to taxpayers.

These two numbers are identical for every revenue-neutral UBI design, where the sum total amount of UBI issued is equal to the sum total amount of new taxes imposed. But for UBI designs where deficit spending is utilized to decrease the tax burden imposed or where the amount of taxes exceeds the UBI distributed in order to reduce the money supply, these two numbers will not be identical.

Where the total amount of net UBI is equal to zero, that will result in every individual being taxed exactly what they received in UBI, and that is the only case where the total cost of UBI is nothing at all, which is an entirely pointless UBI because no one's after-tax income is increased.

Where the total amount of new taxes imposed is equal to zero, that will result in everyone being a net recipient, and that is the only case where the total cost of UBI can be simplified to the amount of UBI multiplied by the number of recipients.

Thus, to understand the actual cost of UBI, one must understand that it actually exists along an axis located between the two extremes of zero and what's commonly believed to be the cost of UBI that's actually the rare special case of newly created money with no new taxes at all to accompany it.

The true cost of UBI will exist somewhere between those two extremes, where it's greater than zero, but less than the cost most people calculate. Realistically speaking, the most likely cost of UBI is somewhere between one-tenth and two-thirds the gross cost that most people think is the actual cost.

Of course, this calculation is challenging to make in practice, because it requires knowing every individual's income and the tax increase on every individual, so an approximation is needed. This can be done by breaking the population into percentiles, or deciles, or even quintiles. To do an approximation by quintile, we'd need to know the tax impact per 20% of the population, and do a summation series of those five groups. That's a lot easier to do.

I performed a calculation like this for a UBI model I did years ago involving a $12,000 UBI paired with a 40% flat income tax, and where the gross cost was $3 trillion, the real cost was around $900 billion, or ~30% of the incorrect calculation most people would make under the belief they need only multiply two numbers.

It's also important to understand that the sigma calculation still isn't a reflection of the true cost of UBI, because spending on UBI will reduce other costs. People with UBI will be healthier, and thus require less medical care. People with UBI will also do less crime, and thus require less incarceration. UBI itself will also negate the need for existing welfare programs and existing tax subsidies to the degree they currently exist. In short, we can spend more to spend less.

The way I like to think about spending more to save money is with a car analogy. Imagine you're the CEO of a car company, and your engine team tells you it's possible to reduce the cost of the transmission by $1,000 per car if you were to spend $100 more per engine. You would be a terrible CEO if you decided to avoid spending $100 more per engine in the belief it would decrease your profit margin.

Basically, the cost of UBI can never be truthfully calculated by assuming that the cost of no UBI is zero. Poverty isn't free. Chronic economic insecurity isn't free. This is why it's been estimated that if we restored the monthly enhanced child tax credit, and made it permanent, the return on investment would be 1000%. By investing $100 billion more in our kids, we'd see an ROI of $1 trillion a year.

Is the cost of reducing child poverty $100 billion even if the sigma cost of the enhanced CTC is $100 billion, if our overall net savings is $900 billion? Or is the true cost actually a $900 billion gain thanks to a smart investment in our kids?

Conclusion

It is commonly misunderstood that to calculate the cost of UBI requires the simple multiplication of two numbers on par with what a student learns when they first learn multiplication. To accurately calculate the cost of UBI requires a bit more effort on par with what a student learns in pre-calculus. It is the summation of two finite arithmetic series, where one is the summation of all positive values, and the second is the summation of all negative values. It is these two summations that together answer the question, "How much does universal basic income cost?"

Do you support independent content like this? Please click the subscribe button and also consider making a monthly pledge or buying a copy of my book.